On Diurnal and Nocturnal Arcs
Published November 24, 2014
Primary Directions are one of the most ancient and renowned predictive methods in Traditional Astrology. Primary Directions fell out of use after the 18th century, but the interest in them has been growing in the latest decades.
In the last week or so, I have been reviewing the Primary Directions module of Elements, my soon-to-be-released Traditional Astrology application. Since Primary Directions can be quite complex mathematically, I needed to compare my results with other available softwares. However, I have noticed that some computer programs have gross errors regarding Primary Directions. Software bugs appear mostly when programs start to get complex.
Therefore, I decided to republish a sequence of articles to present a simpler approach for calculating Primary Directions. This article in specific presents a simpler method for calculating the diurnal and nocturnal arcs of direction, which are essential for calculating Primary Directions.
1 - Defining Diurnal and Nocturnal arcs
In astronomical terms, the arc of an object is the segment, or path, which an object draws in the sky. Therefore, the diurnal arc of a planet is the path drawn above the horizon, from the moment it rises in the East until it sets in the West, while the nocturnal arc is the path drawn below the horizon.
The following picture shows the diurnal arc of the equator and of the Sun for North hemisphere observers.

Sun's diurnal arc in Northern hemisphere for different days of the year.
Each object rises in the East, culminates in the South (or North – for South hemisphere observers) and sets in the West, drawing a diurnal arc. In its arc a planet can be below the equator at southern latitudes, above the equator at northern latitudes or exactly above the equator line.
The diurnal arc is deeply related with the amount of time that a planet spends above the horizon. For instance, for northern observers, when the Sun is north of the equator, days are bigger than nights but when the Sun is below the equator, days are smaller. When the Sun is exactly on the equator, days equal nights and we call it the Equinox.
In terms of arcs, the reasoning is similar. When the Sun is on the equator, both days and nights have the same 12h. Since the Earth spins 360º around its axis in 24 hours, it means that the Sun has a diurnal arc of 180º (360º/2). When the Sun is above the equator, for northern observers, the day time is greater than 12h, therefore its Diurnal arc is greater than 180º. And when the Sun is south of the equator, days are smaller than 12h, and the diurnal arc is lesser than 180º.
As all planets wander more or less near the equator (not to be confused with the ecliptic, though), planets may have diurnal and nocturnal arcs larger or smaller than 180º. In a nutshell, diurnal and nocturnal arcs depend on how far from the equator a planet is.
2 - Defining the Ascensional Difference
To calculate the diurnal and nocturnal arcs of a planet, we must know its Ascensional Difference first. The Ascensional Difference is the angular distance, measured in the equator, between an object rising or setting in the equator, and the horizon.
The following figure shows, for a northen observer, what happens when the Sun rises on the equator and how it compares to its rising times in different times of the year.
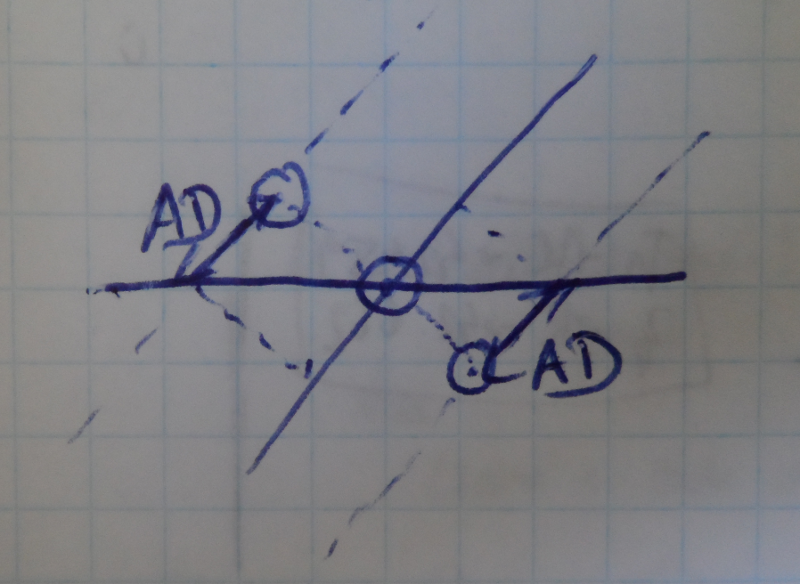
Ascensional differences for the Sun in different times of the year.
The three drawn Suns share the same Right Ascension (RA) values. This means that they are on the same coordinate as measured on the equator line. But when the Sun rises in the equator, the Sun above of the Equator has already rose while the sun below the Equator still has to rise.
For observers in the southern hemisphere, the situation is similar, although the drawings would be skewed to the left and the Ascensional Difference values would switch signals.
For observers in the equator, the situation is like the one on the following figure.
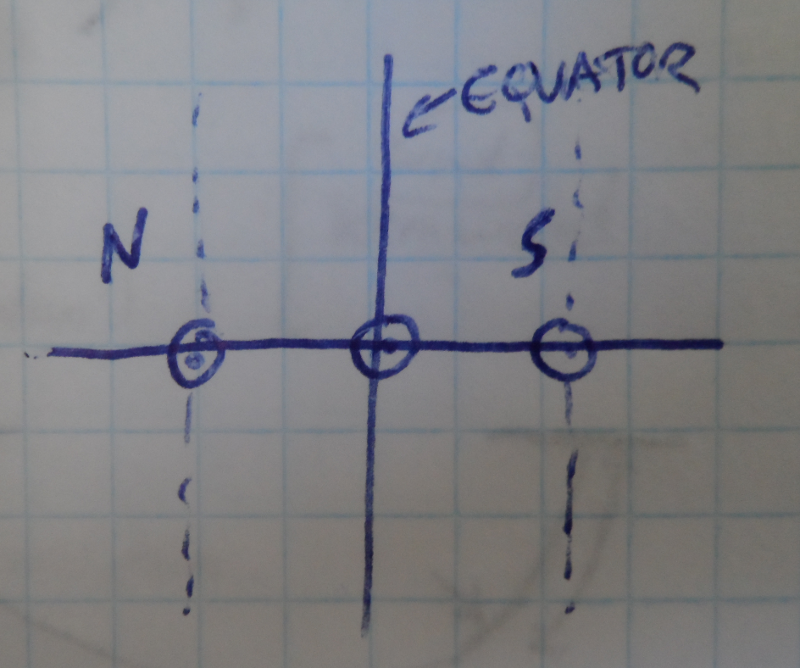
Ascensional Difference for an observer in Earth's equator.
On the Earth's equator, all lines are perpendicular to the horizon. Therefore, the Sun on the equator will rise at the same time as the Suns above and below the equator (north or south). In this case, the Ascensional Difference is zero.
Thus, the Ascensional Difference depends on two factors: the degree between the equator and the horizon, which can be obtained from the observer's latitude, and on the planet's own distance to the equator, known as declination.
3 - Calculating the Ascensional Difference
The following figure shows the relation of angles to obtain the Ascensional Difference AD, where δ is the declination of the object (the distance from the equator – North or South) and Φ is the latitude of the observer.
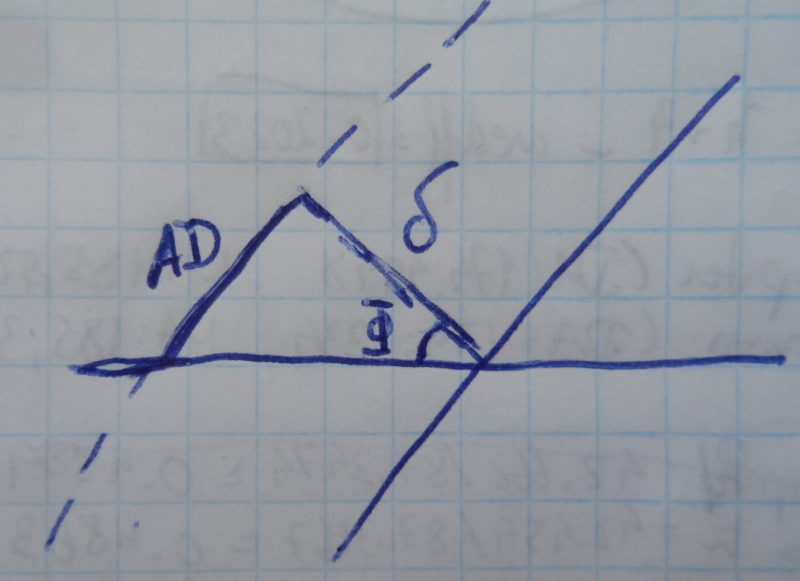
Triangle observed in the Ascensional Difference.
Although this seems an easily solvable triangle-rectangle, it must be solved using spherical trigonometry. Since we live in a spherical planet, those are not straight lines but arcs of larger circles. Therefore, equation:
AD = arcsin(tan δ x tan Φ)
gives us the Ascensional Difference.
4 - Calculating the Arcs
Let us reuse a previous picture:

Ascensional differences when the Sun is rising.
As already explained, any planet on the equator has a diurnal arc of exactly 180º. Assuming that both Suns are equidistant from the equator, the Sun above the equator will have a diurnal arc greater than 180 by one AD while the Sun below the equator will have a diurnal arc smaller than 180º by one AD. In fact, we should add or subtract 2*AD, since we must account for what happens when the Sun sets as well.
Thus, in a general way, the diurnal and nocturnal arcs of an object are given by:
Diurnal Arc = 180º + 2*AD
Nocturnal Arc = 360º – Diurnal Arc
AD = arcsin(tan δ x tan Φ)
We do not need to distinguish between AD's above or below the equator line, because the math does that for us: In the northern hemisphere, positive declinations returns positive values for AD, and the diurnal arc is greater than 180º, while negative declinations results in negative values for AD, and the diurnal arc is less than 180º. Finally, since a full circle has 360º, the nocturnal arc is just the arc that is left after removing the diurnal one.
If one is after semi-arcs, he just needs to divide the arc by two. For instance, a diurnal semi-arc is just one half of the diurnal arc:
Diurnal Semi-Arc = 90º + AD
Nocturnal Semi-Arc = 180º – Diurnal Semi-Arc
5 - Other methods for calculating the arcs
In page 152 of Primary Directions – Astrology’s Old Master Technique, Martin Gansten presents another method for obtaining the semi-arcs. The idea can be summarized in the following figure:
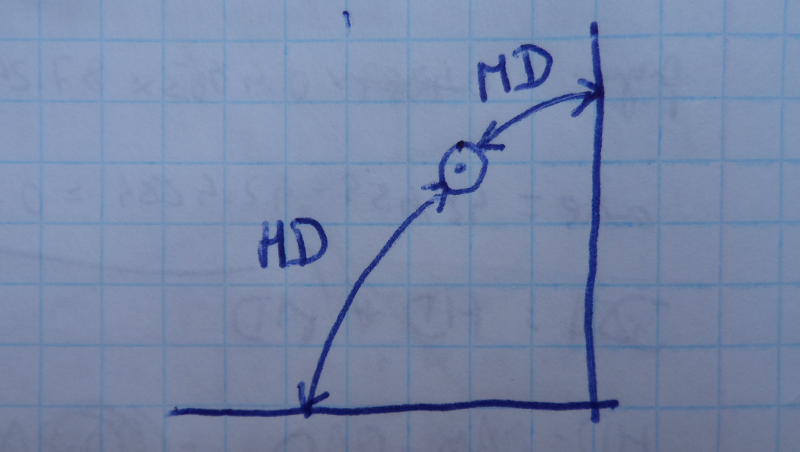
Alternative method for calculating diurnal semi-arcs.
Basically, the diurnal semi-arc of an object can be obtained using the HD (Horizontal Distance – angular distance to the horizon) and the MD (Meridian Distance – angular distance to the meridian). For this method we need more information, such as the RA of the Meridian (RAMC – Right Ascension of MC) and the Oblique Ascensions of the Ascendant and planet.
These are the formulas for the Diurnal semi-arc:
DSA = HD + MD
HD = OA Asc – OA Planet (*)
OA Asc = RAMC + 90
OA Planet = RA Planet – AD
MD = RA Planet – RAMC
(*) In the book, the formula for HD is OA Planet – OA Asc. In the case of the diurnal semi-arc like the one in the figure, this will result in a negative value. To circumvent the "error", the author states that both HD and MD should always be positive.
However, it is easy to show that this complexity is unnecessary:
DSA = HD + MD ↔
DSA = (OA Asc – OA Planet) + (RA Planet – RAMC) ↔
DSA = ((RAMC + 90) – (RA Planet – AD)) + (RA Planet – RAMC) ↔
DSA = RAMC + 90 – RA Planet + AD + RA Planet – RAMC ↔
DSA = RAMC – RAMC + RA Planet – RA Planet</s> + 90 + AD ↔
DSA = 90 + AD
Diurnal Arc = 2*DSA = 2*(90+AD) = 180º + 2*AD
The Right Ascensions of the MC and of the Planet are unnecessary for the calculations.
6 - Conclusions
Diurnal and nocturnal arcs are essential for Primary Directions. In this article I've presented a simple and straightforward way to calculate diurnal and nocturnal arcs. For software developers, this method is more robust than the current formulas, with less chance for errors. For astrologers, less calculations.
In my next article I will describe a generic and simple method for implementing Primary Directions using the proportional semi-arc method.