Primary Directions - A simple approach
Published November 30, 2014
In my previous article I wrote about Diurnal and Nocturnal arcs, which are essential for the calculation of Primary Directions. In that same article it was mentioned that there are alternatives for calculating the arcs, although I believe I've presented the simplest method.
In this article, my purpose is to show the formulas that I have implemented in Elements to compute Primary Directions. This article, similarly to the previous one, is quite technical and not really aimed for people who do not know what Primary Directions are for. For those, I highly recommend the reading of Primary Directions – Astrology’s Old Master Technique by Martin Gansten.
1 - Primary Directions in a nutshell
Primary Directions are one of the most powerful and renowned methods for astrology forecasting. The word primary refers essentially to the primary motion on which this technique is based. The primary motion is basically the daily rotation of the Earth: the Sun, the planets and signs rise in the East, culminate in the South (for an northern observer), set in the West and travel below the horizon only to rise again in the East.
The following image which represents a part of a chart for a certain time and location. Here, the Moon is located somewhere between the Ascendant and the fourth House.
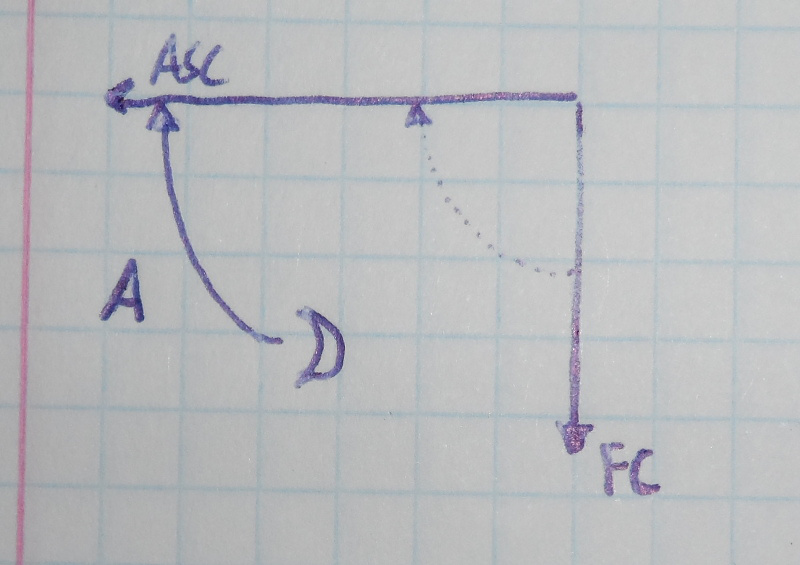
Direction of the Moon to the Ascendant.
Due to the Earth's rotation, after some time the Moon will rise in the East, and will conjunct the Ascendant. In this specific case, to the angular distance between the Moon and the Ascendant (represented by "A" in the figure), we call it the arc of direction of the Moon to the conjunction of the Ascendant. The Moon (Promissor) will eventually arrive at the conjunction with the Ascendant (Significator). In astrological terms, if this arc of direction has for instance 28º, it could mean that somewhere around the 28th year of the nativity, the matters signified by the Moon will affect the native.
Since the arc of direction of the Moon to the Ascendant is an angular distance, one could be tempted to calculate it by measuring the difference between the zodiacal positions of the Moon and the Ascendant. Unfortunately that is not the case! The arc of direction is an angular distance measured in the equator, not in the ecliptic. To understand why, I recommend the third chapter of the Primary Directions book.
2 - Types of directions
The measurement of distances in the equator are not straightforward, and there are three different situations that we have to take into account.
2.1 - Directions to the Ascendant / Descendant
For this case, consider the following figure which shows different ways in which the Moon can conjunct the Ascendant:

Moon to the Ascendant.
In the left, we can see three situations: the Moon is over the equatorial line, the Moon has southern declination (A) and the Moon has northern declination (B). All three Moons share the same position projected in the equator (same Right Ascension), but have different declinations and different nocturnal semi-arcs. The semi-arc A is smaller than B.
In the right sub-figure, we can see what happens later when the Moon rises in the West horizon: when the Moon over the equator rises on the horizon, the Moon in A is still below the horizon while the Moon in B has already rose.
Therefore, if we were to calculate the arc of direction from the Moon to the West horizon, by subtracting the RA (Right-Ascension) of the Ascendant from the RA of the Moon, we would be correct only for the Moon on the equator. For the Moon in A we would need to get an higher value for the arc because the Moon still has to go a little further to reach the horizon. While for the Moon in B, the value for the arc would be too high, and we would have to remove something because the Moon would have already crossed the horizon.
2.2 - Directions to other planets
Finding the arc of direction between two planets is also problematic. For instance, consider this case where we want to calculate the arc of direction from the Moon to the conjunction of Mercury:
Moon to the conjunction of Mercury.
In this specific case we need to find when does the Moon arrive at the same position as Mercury. In fact, we want to know how many equatorial degrees separate them. However, since both planets are not in the same path (nocturnal semi-arcs), the Moon will never reach the same exact spatial position as Mercury. Therefore, what we need is to find when the projected position of the Moon on the equator finds the projected position of Mercury on the equator.
But we now have a problem: which projection should we use? Do we project Mercury to the equator in the horizontal axis (A), along an oblique axis (B) or along a vertical axis (C)?
2.3 - Directions to a meridian
For this last case, the following figure represents the Moon in three different conditions: rising, culminating and setting.
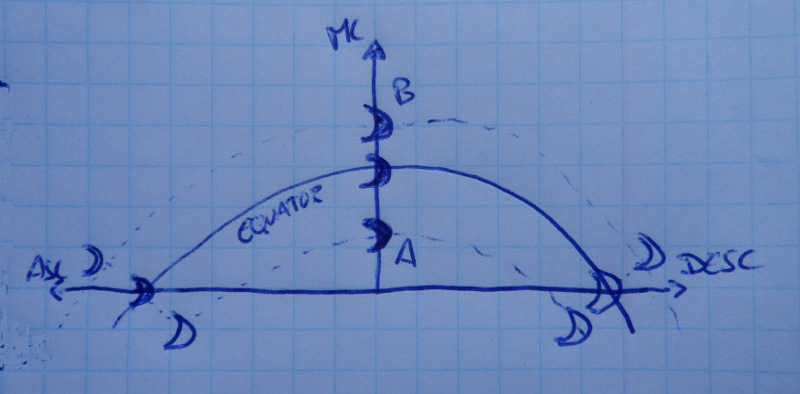
Moon rising, culminating and setting.
The directions to the Ascendant and Descendant have already been explained, but see what happens in the MC: although the three Moons rise and set differently accordingly to their declinations, they all arrive at the same time at the MC.
The calculation of the arc of direction of a planet to a meridian is a simple case, and it consists basically in the difference between the Right Ascensions of the meridian and Promissor.
3 - Common solutions
The previous three problems are usually solved separately:
3.1 - Directions to Meridians
Directions to meridians are the simplest cases. Since the projection of Right Ascensions over meridians are independent of the declination, the arc of direction of a Promissor to the conjunction of a Meridian (MC or IC) is simply given by:
Arc = RA Promissor – RA Meridian
3.2 - Directions to Horizons
Unfortunately, the projections of the planets on the equator are not independent of their declinations when they are near the horizon. Therefore, directions to the horizon cannot be solved simply by subtracting Right Ascensions.
On my previous post about Diurnal and Nocturnal arcs, I introduced the concept of Ascensional Difference (AD). The Ascensional Difference is basically the angular distance between a planet and the horizon. From the AD, we can get the Oblique Ascensions / Descensions (OA/OD) which are essentially the correction of distances considering the horizon.
These are the formulas for calculating the arc of direction of a planet to the Ascendant and Descendant. As you may see, we must consider the Right Ascension of the MC (RAMC) as well as if we are dealing with eastern or western Promissors.
OA Asc = RAMC + 90º
OD Desc = RAMC – 90º
OA (eastern Promissor) = RA – AD
OD (western Promissor) = RA + AD
Arc (East) = OA Promissor – OA Asc
Arc (West) = OD Promissor – OD Desc
3.3 - Directions to other planets
The directions between two planets are the trickiest ones. Although there are different solutions, I will talk about the oldest one, the Proportional Semi-Arc.
So far we have no problem calculating projected RAs on meridian and horizons. However the problem with the directions to planets is how to project them on the equator: should we project the planets like a meridian (vertical projection) or like an horizon (oblique projection)?
I have already talked about Diurnal and Nocturnal arcs of movement: the Diurnal arc is the path a planet does when traveling above the horizon, while the Nocturnal arc is the path he does under the horizon. And a semi-arc is just half an arc.
Consider the following figure which shows Mercury somewhere in its "nocturnal" movement.
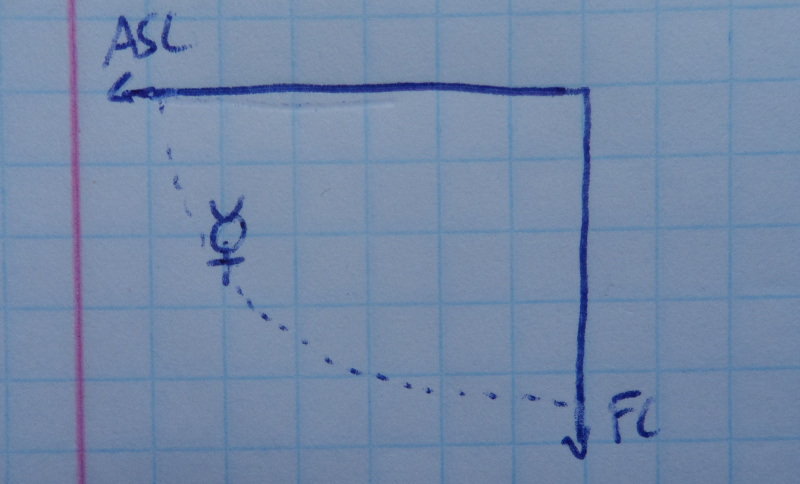
Mercury somewhere in its nocturnal semi-arc.
Mercury is traveling in its nocturnal semi-arc, but he is not in the beginning of its semi-arc (near IC) nor near the end of its semi-arc (it has not yet arrived at the Ascendant). Mercury is somewhere between both, but where exactly?
As mentioned, the projected distances to meridians are the simple cases because of the declination independence. In this case, we can use the direction of Mercury to the IC (which is just the subtraction of Right Ascensions) to find where exactly Mercury is in its semi-arc. Therefore, if the entire semi-arc, from IC to the Ascendant, corresponds to 100%, Mercury has already traveled a certain percentage of it.
The following formulas are used to solve this problem. Here, MD is the Meridian Distance and SA is the Semi-Arc. The Meridian Distance should be calculated from the meridian which is closest to the Significator (MC if the Significator is above the horizon, IC otherwise).
PropDist Significator = MD Significador / SA Significator
Projected MD Promissor = PropDist Significator * SA Promissor
Arc = MD Promissor – Projected MD Promissor
4 - A simpler approach
The problem with the previous solutions are their number. For software developers, as I am, it means three different implementations, while for others it means too many formulas to be used and understood. Either way, I will show that these solutions can be generalized and simplified.
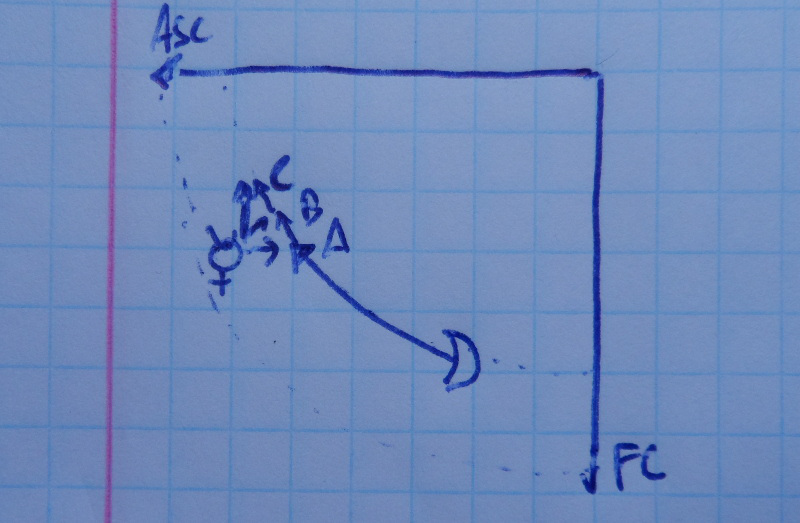
Consider the following figure which represents the direction of the Moon to the conjunction of Mercury:

Moon to the conjunction of Mercury.
Mercury, the Promissor, has already elapsed 60% of its nocturnal semi-arc. Similarly, the Moon has already elapsed 20% of its nocturnal semi-arc. In order for the Moon to reach the same proportional distance as Mercury, the Moon has yet to travel 40% of its own semi-arc.
It should be noted that if we consider positive angles as counter-clockwise, the distances of Mercury and Moon to the IC should be -60% and -20%. Either way, the distance would still be 40%.
If SA is the semi-arc, MD the Meridian Distance, and PropDist the Proportional Distance, the following formulas allows us to calculate the arc of direction for any two generic points:
PropDist Significator = MD Significator / SA Significator
PropDist Promissor = MD Promissor / SA Promissor
Arc = (PropDist Promissor – PropDist Significator) * SA Promissor
(*) The calculations of the semi-arcs are on the previous article, and the Meridian Distance is just the subtraction of Right Ascensions.
The meridian distances should be to the one closest to the Significator (MC if the Significator is above the horizon, IC otherwise). This is just a reformulation of the semi-arc method, but as I will show, it can be generalized for the three different cases:
4.1 - Adequacy to the problem of directions to another planet
Arc = (PropDist Promissor – PropDist Significator) * SA Promissor
Arc = (MD Prom / SA Prom – PropDist Signif) * SA Prom ↔
Arc = MD Prom - PropDist Signif * SA Prom ↔
Arc = MD Promissor – Projected MD Promissor
Which is the same formula as stated in section 3.3.
4.2 - Adequacy to the problem of directions to the Ascendant and Descendant
The solution to this problem considers that the Ascendant (or the Descendant) are Significators which have traveled 100% of their semi-arcs. The following solution applies to the Ascendant:
Arc = (PropDist Promissor – PropDist Significator) * SA Promissor
Arc = (PropDist Promissor – 1.0) * SA Prom ↔
Arc = (MD Prom / SA Prom – 1.0) * SA Prom ↔
Arc = MD Prom – SA Prom ↔
Arc = (RA Prom – RA Meridian) – (90 + AD Prom) ↔
Arc = RA Prom – AD Prom – RA Meridian – 90 ↔
Arc = (RA Prom – AD Prom) – (RA Meridian + 90) ↔
Arc = OA Promissor – OA Ascendant
For the Descendant, one has to consider that the it is a point that has traveled -100% of its diurnal semi-arc. The negative number comes from considering clockwise angles as negative.
Arc = (PropDist Promissor – PropDist Significator) * SA Promissor
Arc = (PropDist Promissor – (-1.0)) * SA Prom ↔
Arc = (MD Prom / SA Prom + 1.0) * SA Prom ↔
Arc = MD Prom + SA Prom ↔
Arc = (RA Prom – RA Meridian) + (90 + AD Prom) ↔
Arc = RA Prom + AD Prom – RA Meridian + 90 ↔
Arc = (RA Prom + AD Prom) – (RA Meridian – 90) ↔
Arc = OD Promissor – OD Descendant
Both are the same formulas as stated in section 3.2.
4.3 - Adequacy to the problem of directions to a Meridian
The solution for directions to meridians considers that a meridian is a Significator which as traveled 0% of its semi-arc:
Arc = (PropDist Promissor – PropDist Significator) * SA Promissor
Arc = (PropDist Promissor – 0.0) * SA Prom ↔
Arc = (MD Prom / SA Prom) * SA Prom ↔
Arc = MD Prom ↔
Arc = RA Promissor – RA Meridian
Which is the same formula as stated in section 3.1.
5 - Conclusions
Although there are three separate cases that must be considered for the calculation of Primary Directions, they can be all solved using a single method. This generic method allows for software developer, or astrologers willing to do the calculations by hand, to calculate Primary Directions with less chance for errors.